The Kelly Criterion is a mathematical formula to determine the optimal fraction of one's assets to allocate to a bet or investment. It's designed to maximize the long-term growth rate of wealth by considering the probability of winning and the potential return or loss.
Purpose
The Kelly Criterion aims to find the "optimal" bet size that maximizes expected wealth growth over time.
Formula
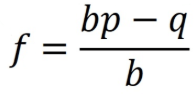
The formula is often expressed as: 𝑓 = (b * p) - q / b, where:
- 𝑓 is fraction of your capital to invest
bis the potential reward per unit bet (e.g., if you bet $1 and win $2, b = 2).pis the probability of winning. (if the probability of winning is 80% = 0.8)qis the probability of losing (q = 1 - p).- G = gain multiple on win ( 400% multiplied = 4 times of the principle)
- L = loss multiple on loss (50% loss = 0.5 times of the principle)
Where:
- 𝑓 = ?
-
p =0.8 (probability of winning )
-
q =0.2 (probability of loss)
-
G =4.0 (gain as a multiple of the investment; 400% return)
-
L = 0.5 (loss as a fraction of the investment; 50% loss)
<Reward and Risk Ratio>
Win: Lose = 4: 0.5 (Very Good Ratio)
Plugging in the values:
f∗=0.50.8−4.00.2=1.6−0.05=1.55
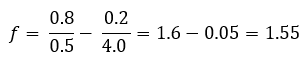
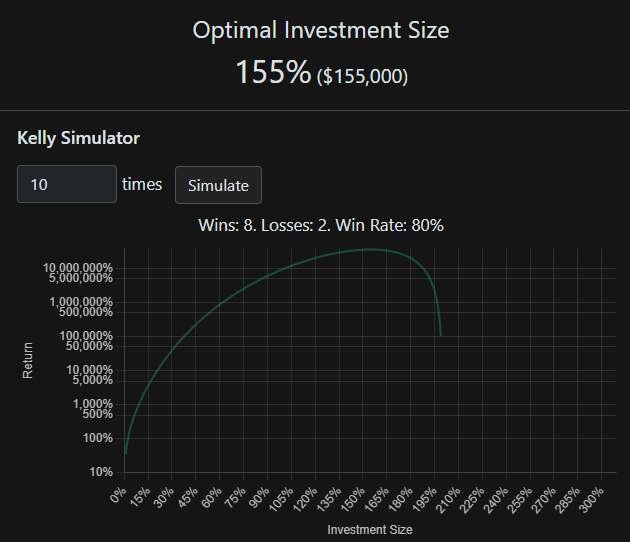
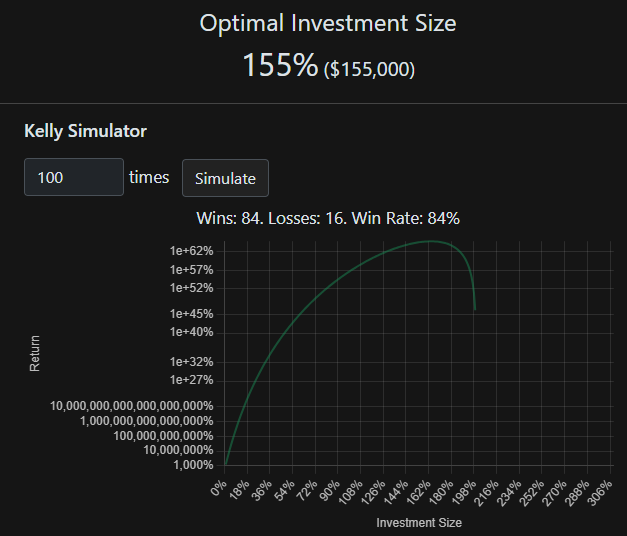
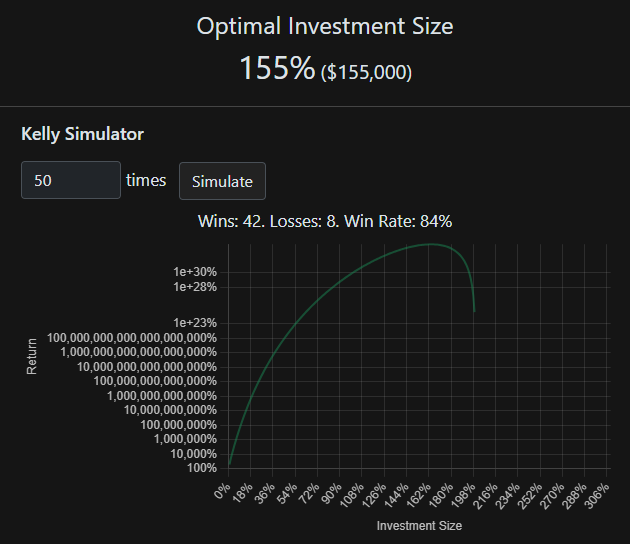
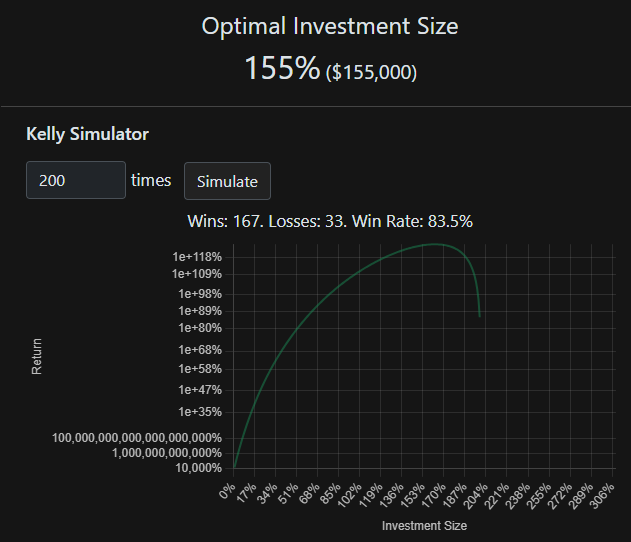
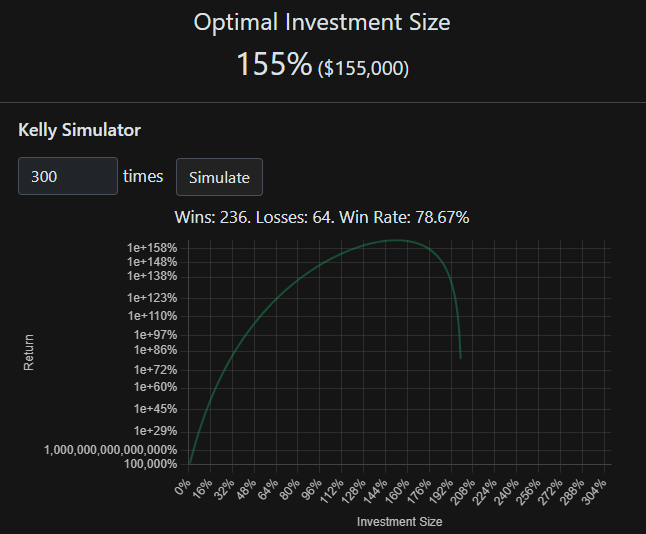
𝑓 = 1.55 = 155% of the initial principal is the optimal betting. If $100,000 is the initial principal, 1.55 x $100,000 = $155,000
With a leverage of 1.55 x, $155, 000 is the optimal bet.